向量和矩阵基础
在线性代数中,向量和矩阵是重要的概念。向量是一种特殊的矩阵,矩阵也是一种特殊的向量。一个 n 维向量,可以写成 n x 1 的矩阵,或者 1 x n 的矩阵,分别叫做列向量与行向量。单个向量可以视为一阶矩阵,多个向量组合在一起就组成了矩阵。
向量的定义:
向量,也称为欧几里得向量、几何向量或矢量,既可以从代数角度去理解,也可以从几何角度去理解。
- 代数角度:向量是一个有序数组,n 维向量中存了 n 个数,有先后次序之分
- 几何角度:向量是一个带方向(Direction),有长度(Magnitude)的箭头(长度也称为模)
向量没有绝对位置,也就是说当它出现在某个坐标系中,起点在何处并不会影响它本身。为了让向量的表达和计算更直观和方便,我们一般会将其起点设定在坐标系原点中。
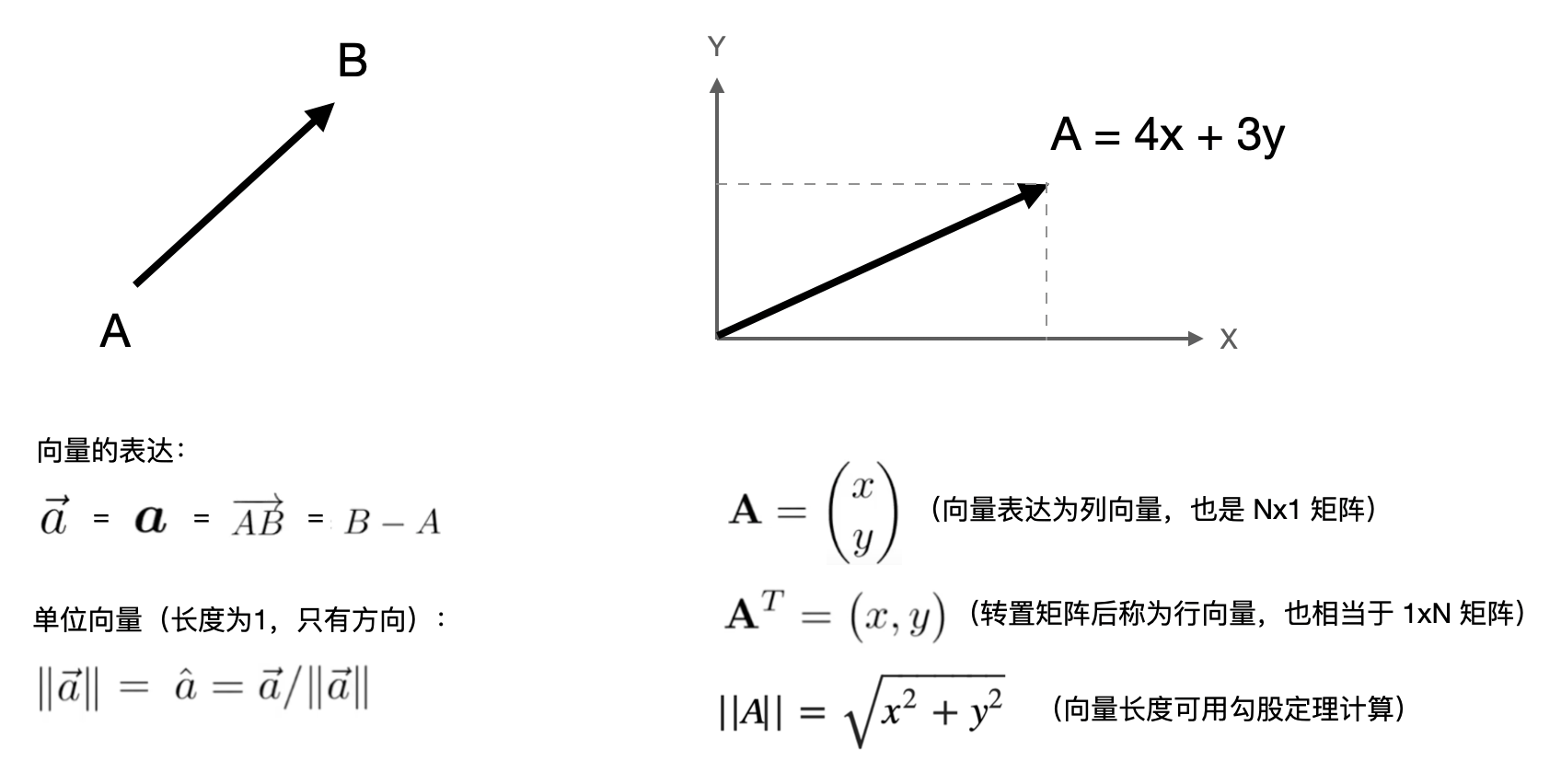
向量与点都可以表达为 (x, y) 或 (x, y, z),虽然数学形式上相等,但几何意义完全不同:
- 点:有位置,没有实际大小或方向
- 向量:无位置,有实际大小和方向
- 联系:任何一个点都可以看作是从原点出发的向量
向量的计算
向量的计算需要区分数学意义和几何意义,特别是涉及到实际 3D 场景的构建时,从几何意义的角度出发,能简化我们的理解成本。
1. 向量加减法计算
向量的加减法在代数或数学角度就是对应的坐标进行加减运算,如下所示:
- 计算公式:(ax, ay) + (bx, by) = (ax+bx, ay+by)
- 加法:对应位置相加,例:(1, -4) + (7, 3) = (8, 1)
- 减法:对应位置相减,例:(-3, 6) - (-4, 3) = (1, 3)
而从几何视角来看,假设有向量 a = (ax, ay) 和 b = (bx, by) ,a 向量加 b 向量最后得到的是从 a 向量起点到 b 向量结束之间形成的新的向量;a 向量减 b 向量后得到的是从 b 结束点指向 a 结束点的新向量。
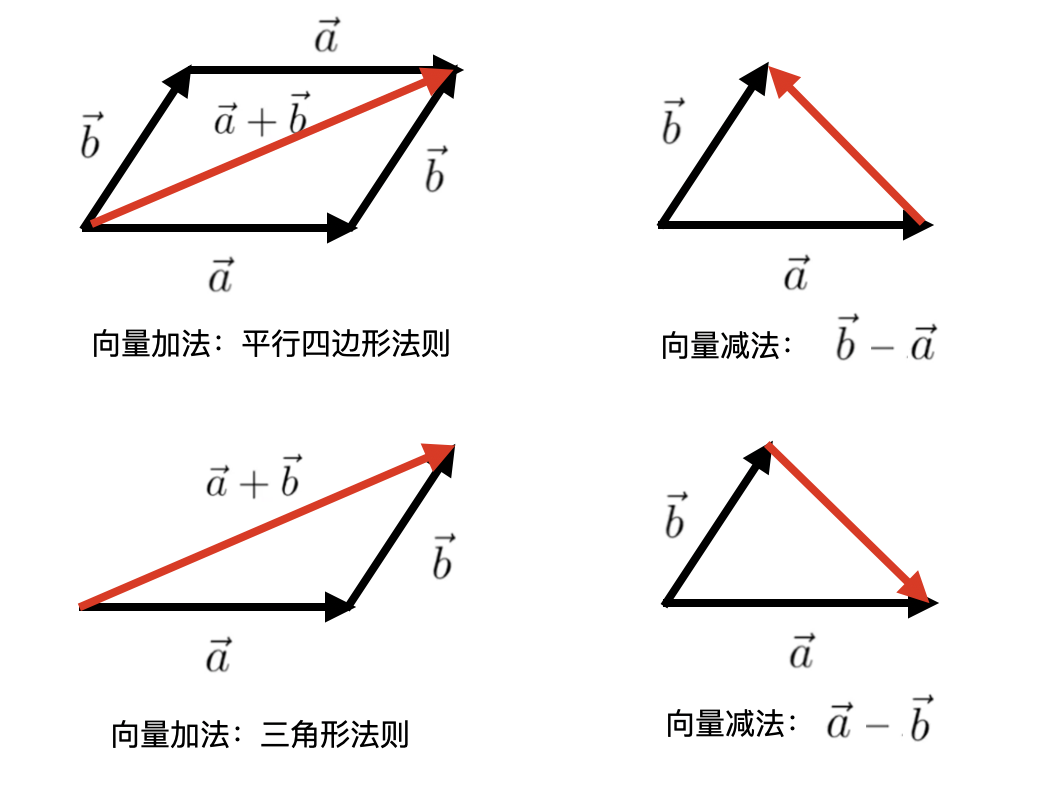
2. 向量点乘/点积计算
向量点乘几乎是应用的最广也最重要的向量运算了。其数学意义即分量乘积的和,最终计算出来的值是一个标量(常数):
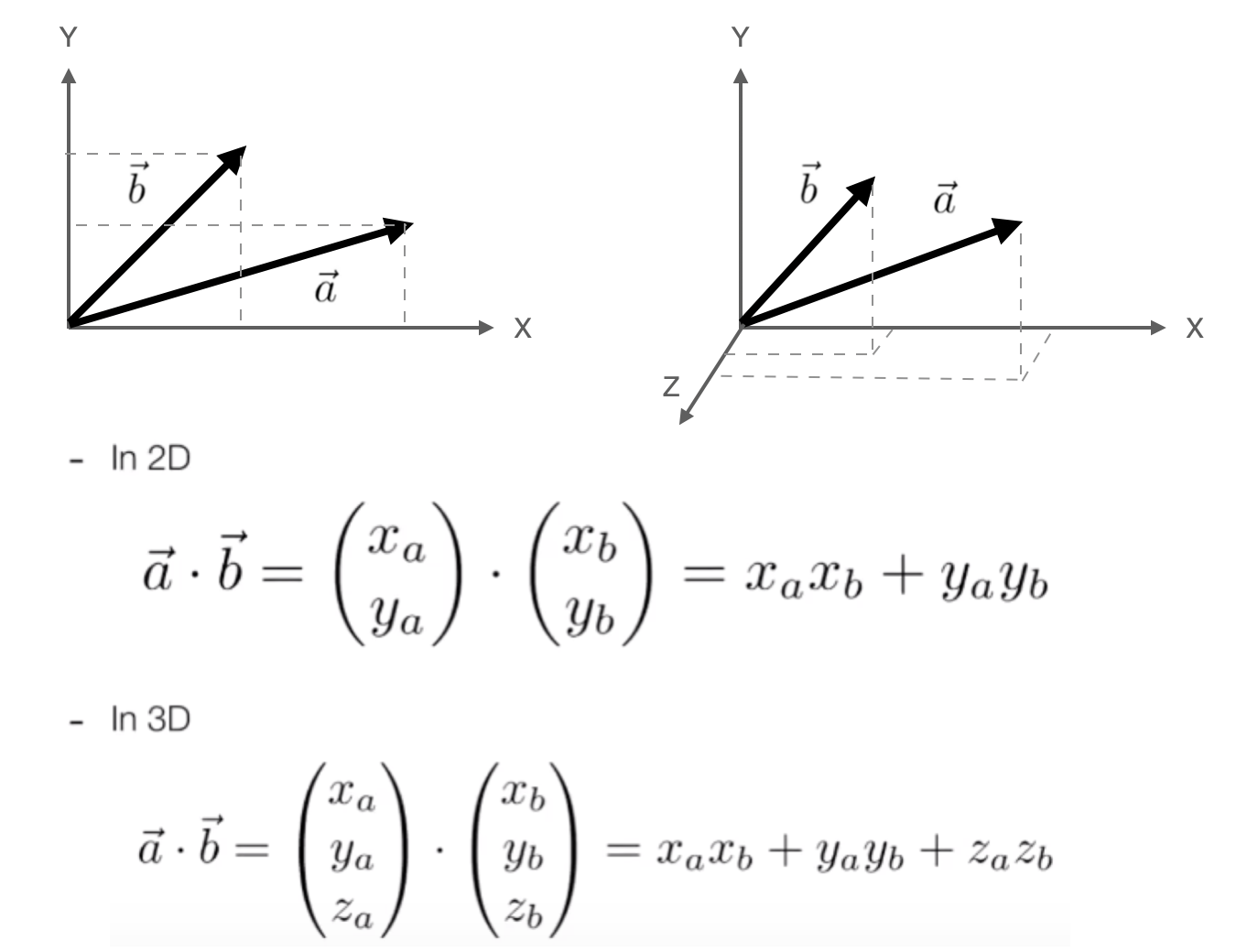
其几何意义则更加丰富,从上面的公式可知点乘的结果是一个常数。点乘结果描述了两个向量的「靠近」程度,值越大,夹角越小;值为 0,刚好垂直;值为负,方向相反。基于此,可以使用点乘来做以下事情:
- 计算光照入射向量和物体表面法线向量的点乘,实现最基础的光照着色
- 计算两个向量的相向和反向关系,便于做模型剔除、背面消除等优化手段
- 计算两条向量彼此的「投影」长度,由此衍生出 Ray Marching 的基础算法(以后会提及)

PS:上图表示的是向量点乘的几何运算,其数学运算满足交换律、结合律和分配律。
下面的 Demo 就是点乘在实现太空球体边缘光的效果中的应用,通过摄像头视角和球体法线点乘得到菲涅尔效果,再通过光线和球体法线点乘得到光照效果,最后两者结合得到基于摄像头移动的球体边缘光照效果:
See the Pen Inner Glow (directional fresnel) by ShaderFans (@shaderfans) on CodePen.
3. 向量叉乘/叉积计算
叉乘的数学意义即:分量交叉相乘再相减,结果仍然是一个向量,新向量的长度就是两个向量形成的平行四边形的面积。
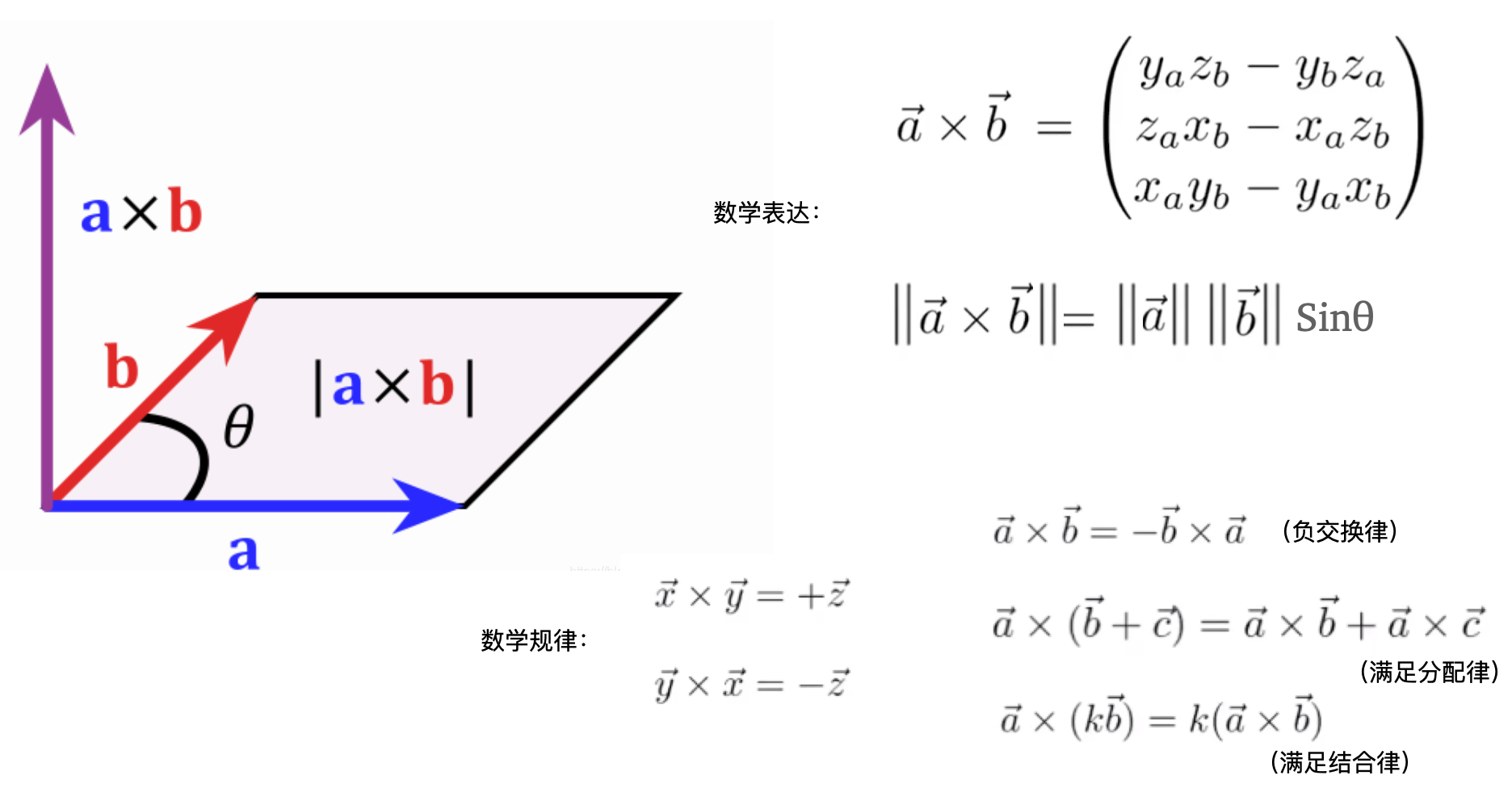
叉乘/叉积的几何意义:
- 判定向量的左右关系以及内外关系
- 叉乘得到的向量垂直于原来的两个向量(法向量)
- 因为垂直与两个向量的向量存在两个,可以用右手法则判断向量的正反
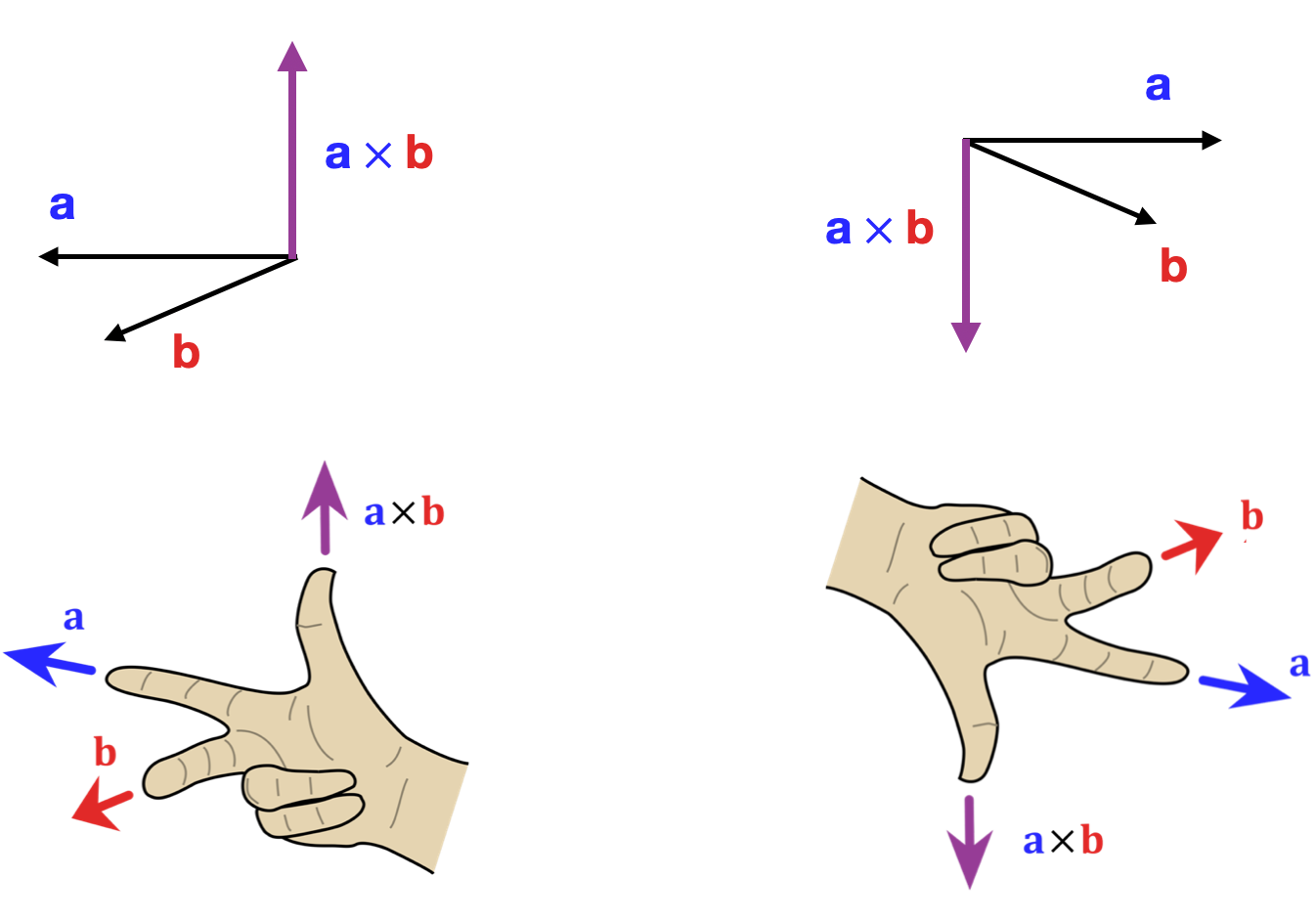
下面的 Demo 展示了将两个向量的叉乘所得到的法向量作为旋转轴,两个向量点乘所得到的值作为旋转角度,实现了球体在不同地点之间的旋转:
See the Pen Rotate between points by ShaderFans (@shaderfans) on CodePen.
矩阵的定义:
将一些元素排列成若干行,每行放上相同数量的元素,就是一个矩阵(Matrix)。数学上,一个 m × n 的矩阵是一个由 m 行和 n 列元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或数学式。
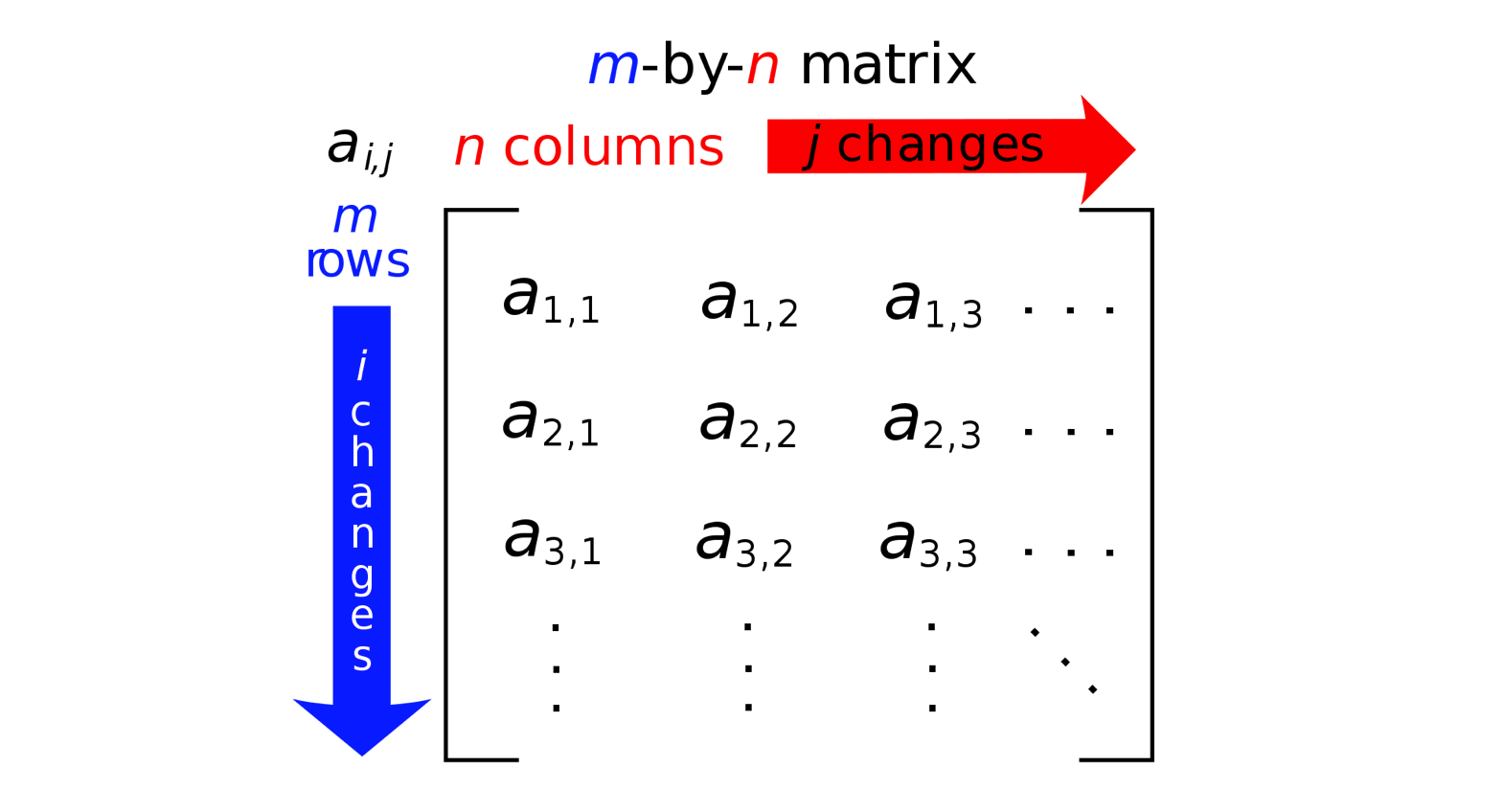
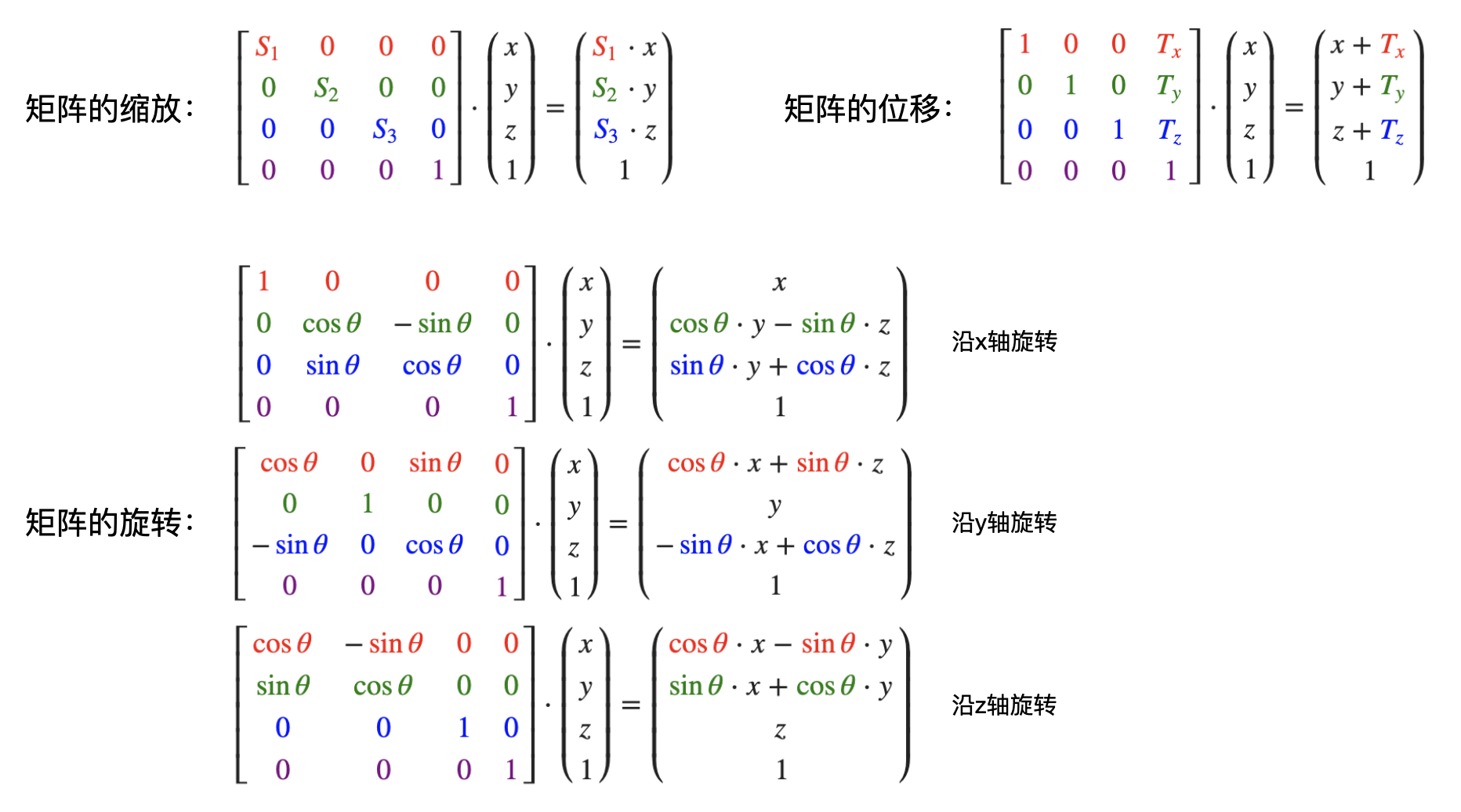
以下列举矩阵的基本计算,需要特别注意的是,矩阵乘法一般不满足交换律:AB ≠ BA:

了解完矩阵的基本规律后,我们就可以利用一些已经构建好具有一定几何意义的矩阵来对我们的原有矩阵进行变换:
行主序和列主序
首先需要明确的是:无论 Direct3D 还是 OpenGL,所表示的矢量和矩阵都是依据线性代数中的标准定义的,而其差别只是「矩阵的存储方式」。在编程时,需要借助数组来存储矩阵数据,此时就有了「行主序」与「列主序」两种区别:
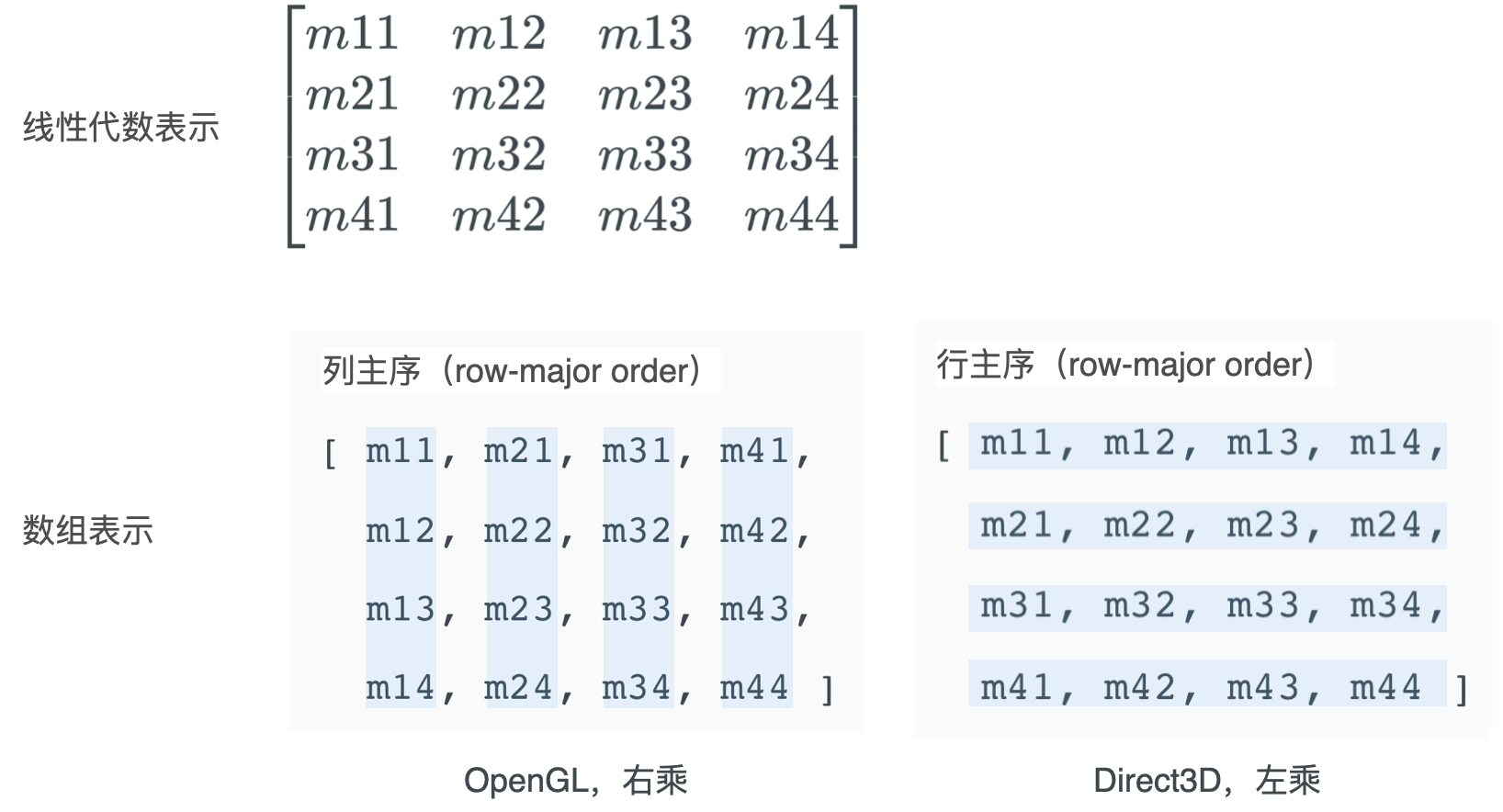
由行主序与列主序列衍生出了另外一个问题:矩阵乘法顺序和规则。
矩阵乘法在线性代数中的定义是确定的,然而在不同的实现中出现了「左乘」(从左往右乘)和「右乘」(从右往左乘)的区别,或者叫做「前乘」(pre-multiplication),「后乘」(post-multiplication)。
这个规则取决于向量 Vector 的表示形式,即行向量还是列向量。如果是行向量,其实就是一个行矩阵。那么表示线性代数意义的「行x列」,就是前乘。矩阵乘法也是如此。
D3D 是行向量,行优先存储,OpenGL 是列向量,列优先存储。同一个矩阵用 D3D 存储还是用 OpenGL 存储虽然不同,但是变换的结果却是相同,因为 OpenGL 变换向量是把向量视作列向量,并同矩阵的每一列相乘,用来实现线性代数中同一个变换。