仿射变换

仿射变换（Affine transformation），又称仿射映射，是指在几何中，对一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。

—— 仿射变换 - Wikipedia

仿射变换即经过对坐标轴的放缩，旋转，平移后原坐标在在新坐标域中的值，或者可以理解为：仿射变换 = 线性变换 + 平移。由于线性变换不改变坐标原点，而平移需要改变坐标原点，为了用同样的形式来表述线性变换和平移这两种不同的操作，人们引入一个新的维度 w 用来帮助表示平移，也就是齐次坐标。

仿射变换因何而来？它是向量空间变换的数学表达。从本文开始，我们将逐渐接触线性代数这门学科，它主要体现在矩阵运算上。为何要有矩阵运算？因为矩阵就是向量的一种表现形式，它可以帮助我们简化计算。

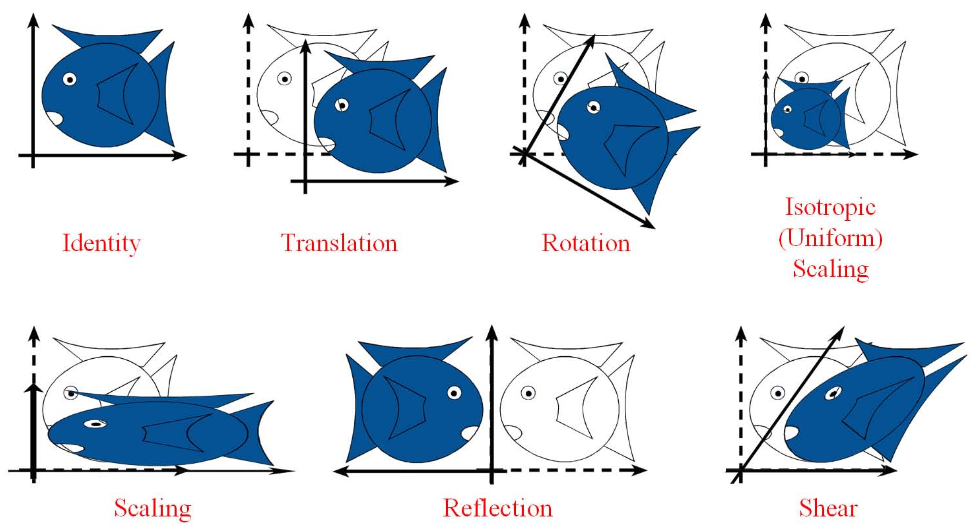
由于文章不会从无到有介绍线性代数，只会使用其定义和结论，建议对该知识点陌生的同学们先看看 《线性代数的本质》 或者闫令琪在《现代计算机图形学入门》 P2/3/4 中对线性代数和仿射变换的总结，这里也有我对知识点的一些记录：向量和矩阵基础。

由简入繁：位移

先从最简单的平移说起，位移就是坐标系在 X 和 Y 轴上的位置偏移，我们只需要将对坐标做简单的加减法运算即可实现（案例中使用到了简单的定时器用于制作动画，下一篇就会讲到，可先忽略）：

See the Pen 2d transform - translate - 001 by ShaderFans (@shaderfans) on CodePen.

// 这种方式并无用到矩阵运算，只是简单的坐标数值加减
uv.x += sin(u_time)*.3;
//uv.y += cos(u_time)*.3;

当我们引入仿射变换之后，进行的就是矩阵运算，如下所示（效果没有变化）：

See the Pen 2d transform - translate - 002 by ShaderFans (@shaderfans) on CodePen.

核心的代码如下：

mat3 translate(vec2 t) {
    return mat3(1.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
                t.x,  t.y, 1.0);
}

void main() {
    ...
    vec2 movement = vec2(sin(u_time)*.3, 0.);
    vec3 xy = vec3(uv, 1.);  // 补充一个 z 坐标
    vec3 tx = translate(movement) * xy;   // 矩阵相乘
    ...
}

举一反三：其他矩阵

下面的案例一次性把四种仿射变换类型一起使用：

See the Pen 2d transform - translate - 002 by ShaderFans (@shaderfans) on CodePen.

将矩阵变换封装成了函数，便于根据实际需要调用：

// Construct a 3x3 matrix for a 2D rotation
mat3 rot(float theta) {
    float c = cos(theta);
    float s = sin(theta);
    return mat3(c, -s, 0.0,
                s, c, 0.0,
                0.0, 0.0, 1.0);
}

// Construct a 3x3 matrix for a 2D axis-aligned scale
mat3 scale(vec2 s) {
    return mat3(s.x, 0.0, 0.0,
                0.0, s.y, 0.0,
                0.0, 0.0, 1.0);
}

// Construct a 3x3 matrix for a 2D shear
mat3 shear(vec2 k) {
    float t = tan(k.x);
    float t2 = tan(k.y);
    return mat3(1.0, t, 0.0,
                t2, 1.0, 0.0,
                0.0, 0.0, 1.0);

}

// Construct a 3x3 matrix for a 2D translation
mat3 translate(vec2 t) {
    return mat3(1.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
                t.x, t.y, 1.0);
}

3D 空间变换

在构建 3D 场景时，矩阵有着非常重要的作用。在 3D 世界中存在多种不一样的坐标空间：

• 局部空间（Local Space，或者称为物体空间 Object Space）
• 世界空间（World Space）
• 观察空间（View Space，或者称为摄像机空间 Camera Space、视觉空间 Eye Space）
• 裁剪空间（Clip Space）
• 屏幕空间（Screen Space）

再详细介绍每个坐标空间的特点：

1. 局部空间：

局部空间或物体空间内，物体的坐标称为局部坐标 (Local Coordinate)，它只和模型本身有关系。举个例子：在创建圆球时，一般将球心作为参考点来创建球体上的各个点，实际上就是构建了一个以球心为原点的参考坐标系。局部空间存在的意义就是作为模型构建和变换的参考坐标系。

2. 世界空间：

世界空间中，物体的坐标称为世界坐标 (World Coordinate)，它定义了统一的空间坐标，让所有物体可以放置其中，拥有坐标之后，物体之间存在了联系。举个例子，银河系可以理解为一个世界空间，在没有银河系之前，每个星球都是相互独立没有联系的，只有当所有星球摆放在银河系后，星球之间才有了相对位置。

3. 观察空间：

观察空间中的坐标称为观察坐标 (View Coordinate)，即从摄像机的视角所观察到的空间。我们通过 WebGL 在屏幕上展现给用户的内容并不是世界空间中摆放的全部内容，而是通过摄像机来模拟用户的眼睛所呈现的场景。

4. 裁剪空间：

裁剪空间中的坐标称为裁剪坐标 (Clip Coordinate)，由于摄像机有朝向，也有视野范围，用户并不能看到所有场景中的物体，在该视野范围内看到的空间就是裁剪空间，所有在视野范围之外的东西都要被剔除。

5. 屏幕空间：

屏幕空间的坐标称为屏幕坐标 (Screen Coordinate) ，它是整个空间变换流程中的最后一环，这里的空间可以理解为终端设备（手机、平板等）的分辨率，由上一步得到的标准化坐标（0~1）映射到具体的分辨率像素中。

而坐标从一个空间到另一个空间则需要变换矩阵来完成这一过程：

• 模型矩阵（Model Matrix）
• 观察矩阵（View Matrix）
• 投影矩阵（Projection Matrix）

下面的这张图展示了整个流程以及变换矩阵在参与环节：

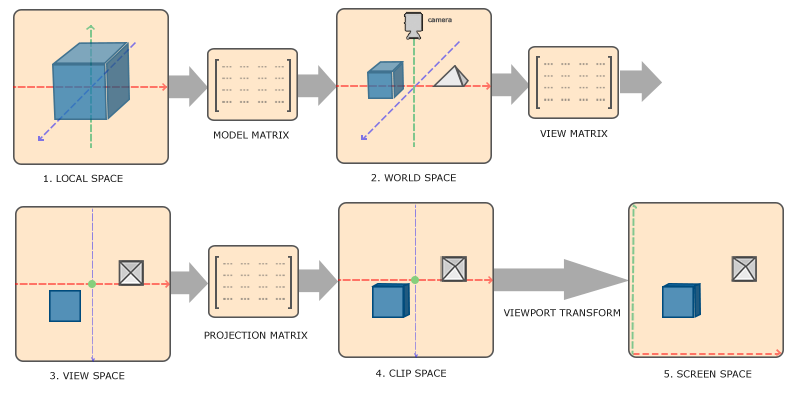
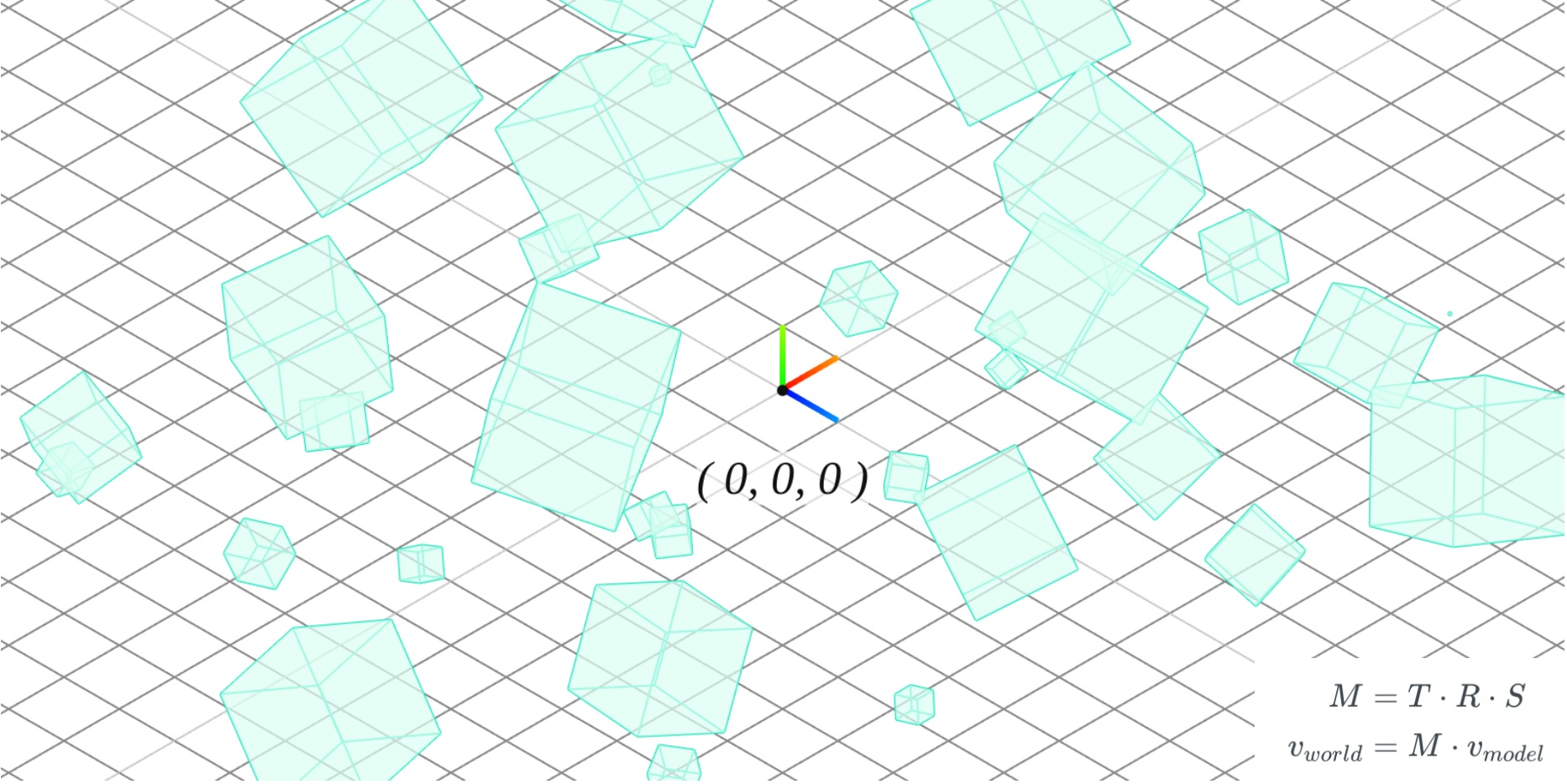
1. Local Space → Model Matrix → World Space：

当所有物体初次放置入世界空间时，它们的初始位置都是一样的——世界的原点 (0.0, 0.0, 0.0) ，我们需要为每一个物体定义一个位置，从而能在更大的场景中合理的摆放让它们。模型矩阵 (Model Matrix) 的作用就是通过对物体进行位移、缩放、旋转等操作将其摆放到场景中的不同位置，从局部空间（图上）变换到世界空间（图下）。

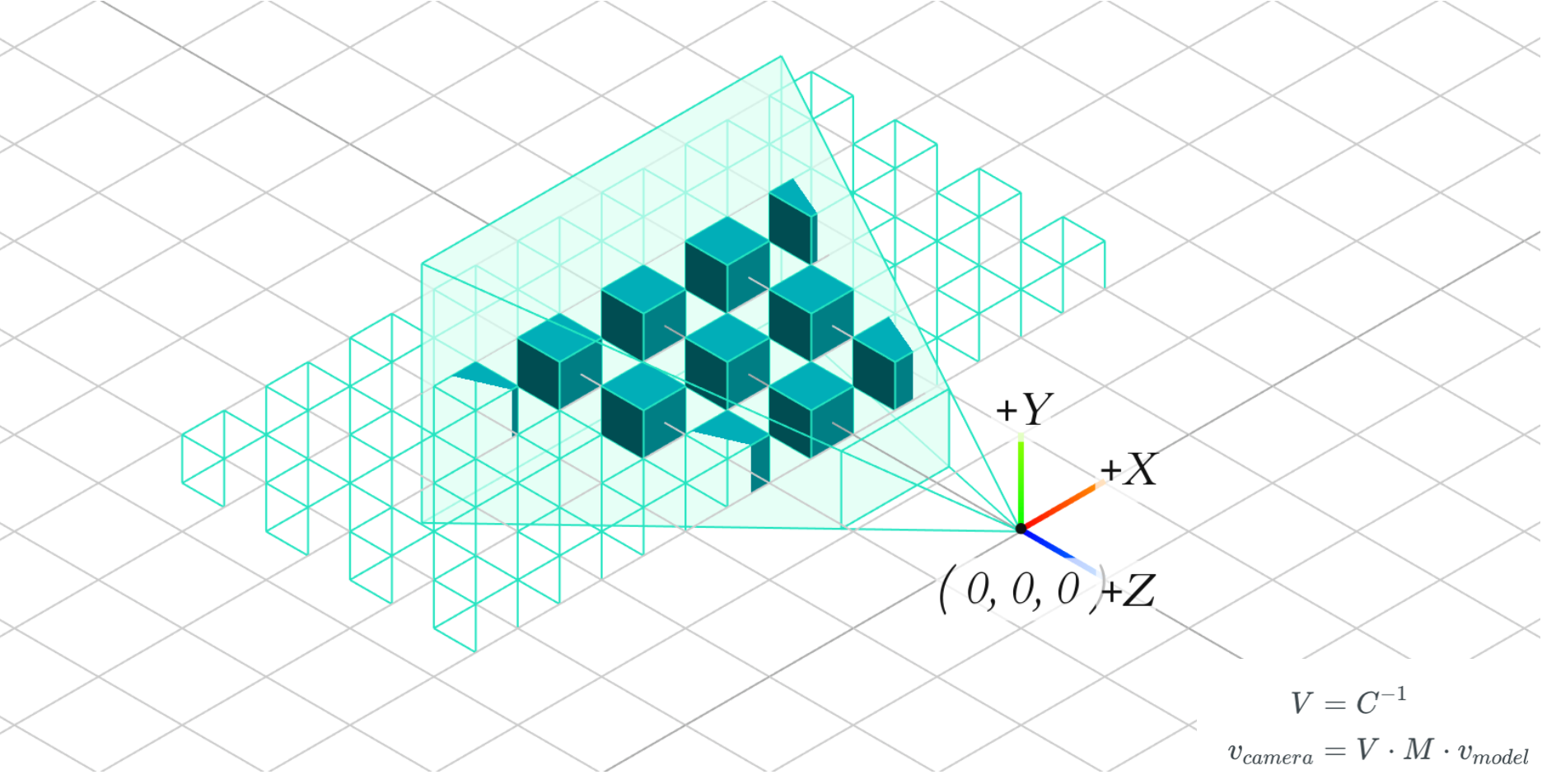
2. World Space → View Matrix → View Space：

在 3D 场景中，我们会借助「摄像机」来定义用户所观察的视角和位置。观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。也就是说该空间下所有物体的坐标都应该相对于相机 Camera 做变换。

在观察空间中，相机的位置就是空间的原点，即 (0, 0, 0)，同时朝向是 -Z 轴。相机本身也拥有 Model Matrix，而相机的 Model Matrix 的逆矩阵就是观察矩阵 (View Matrix)。只要是在同一个世界空间下，任意物体乘以相机的逆矩阵（观察矩阵），都可以变换到观察空间中。

根据逆矩阵的基本原理：矩阵 M 和它的逆矩阵相乘，得到的是单位矩阵。逆矩阵经常被用于得到某个点相对于新参照系的位置。如果两个矩阵都在同一坐标系中，就可以得到某个矩阵相对于另外一个矩阵的变换。

3. View Space → Projection Matrix → Clip Space：

为了将顶点坐标从观察变换到裁剪空间，我们需要定义一个投影矩阵 (Projection Matrix)，它指定了一个范围的坐标，比如在每个维度上的 -1000 到 1000。投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围 (-1.0, 1.0)。所有在范围外的坐标不会被映射到在 -1.0 到 1.0 的范围之间，所以会被裁剪掉。

由投影矩阵创建的观察箱 (Viewing Box) 被称为平截头体 (Frustum)，将观察坐标变换为裁剪坐标的投影矩阵可以为两种不同的形式，每种形式都定义了不同的平截头体。我们可以选择创建一个正射投影矩阵 (Orthographic Projection Matrix) 或一个透视投影矩阵 (Perspective Projection Matrix)。

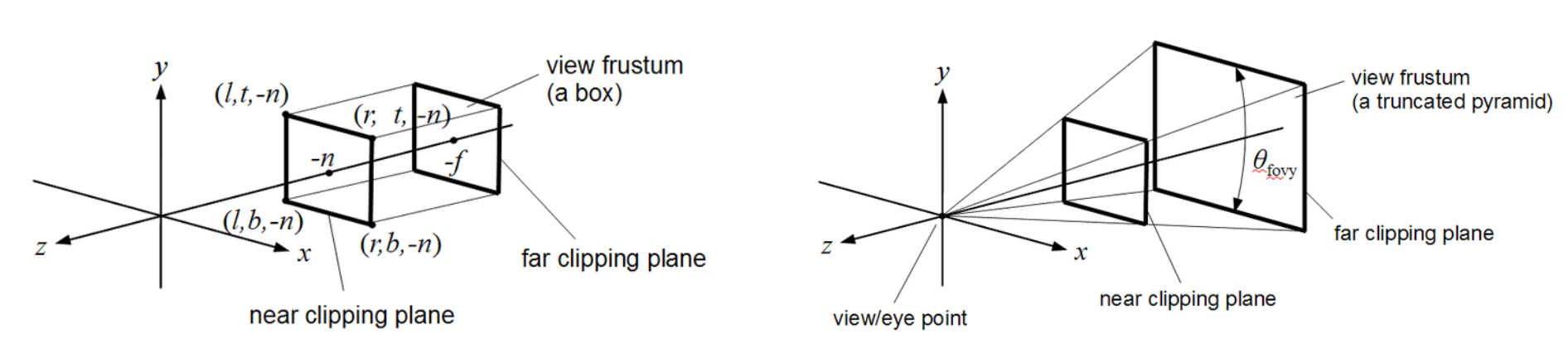
每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上，将特定范围内的坐标转化到标准化设备坐标系的过程（而且它很容易被映射到 2D 观察空间坐标）被称之为投影 (Projection)，因为使用投影矩阵能将 3D 坐标投影 (Project) 到很容易映射到 2D 的标准化设备坐标系中。

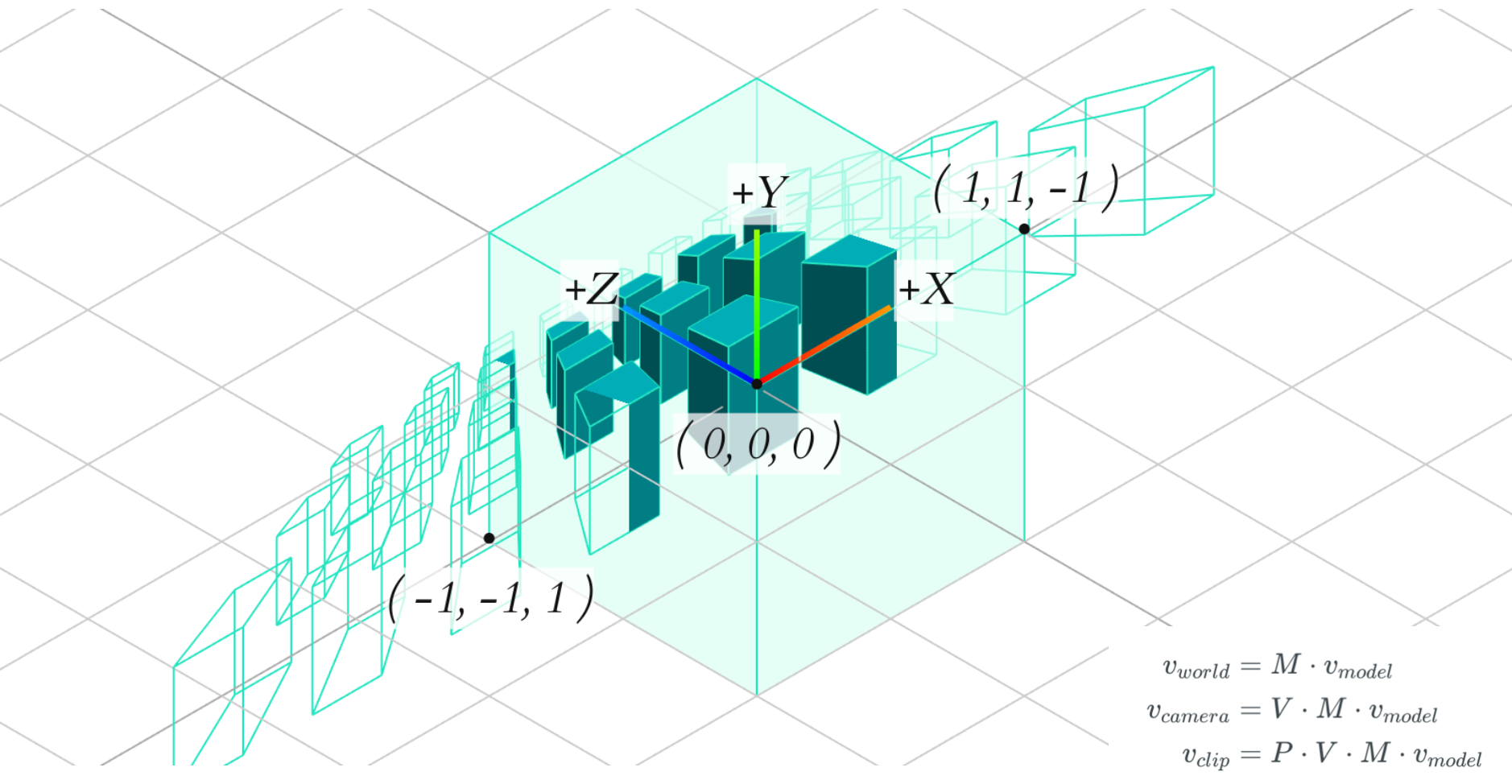
一旦所有顶点被变换到裁剪空间，最终的操作——透视除法 (Perspective Division) 将会自动执行，在这个过程中我们将位置向量的 x，y，z 分量分别除以向量的齐次 w 分量；透视除法是将 4D 裁剪空间坐标变换为 3D 标准化设备坐标（NDC: normalized device coordinates）的过程。

4. Clip Space → Viewport Transform → Screen Space：

经过上一步的裁剪和透视除法得到了标准化设备坐标 NDC，此时的 xyz 坐标都是 0~1 的归一化数值，而最终屏幕的具体分辨率并非 0~1，所以需要有一个映射转换（缩放、平移等）的过程，这个过程就是 Viewport Transform，转换后的坐标将呈现于屏幕空间中。

通过下面视频直观的理解几种空间的变换：

下面的图片展示了顶点着色器和片元着色器在什么阶段介入以及结束：

PS：对 Threejs 感兴趣的同学们也可以看看番外篇：Three.js 空间转换与矩阵运算。